Absolute Value Inequalities With Two Variables

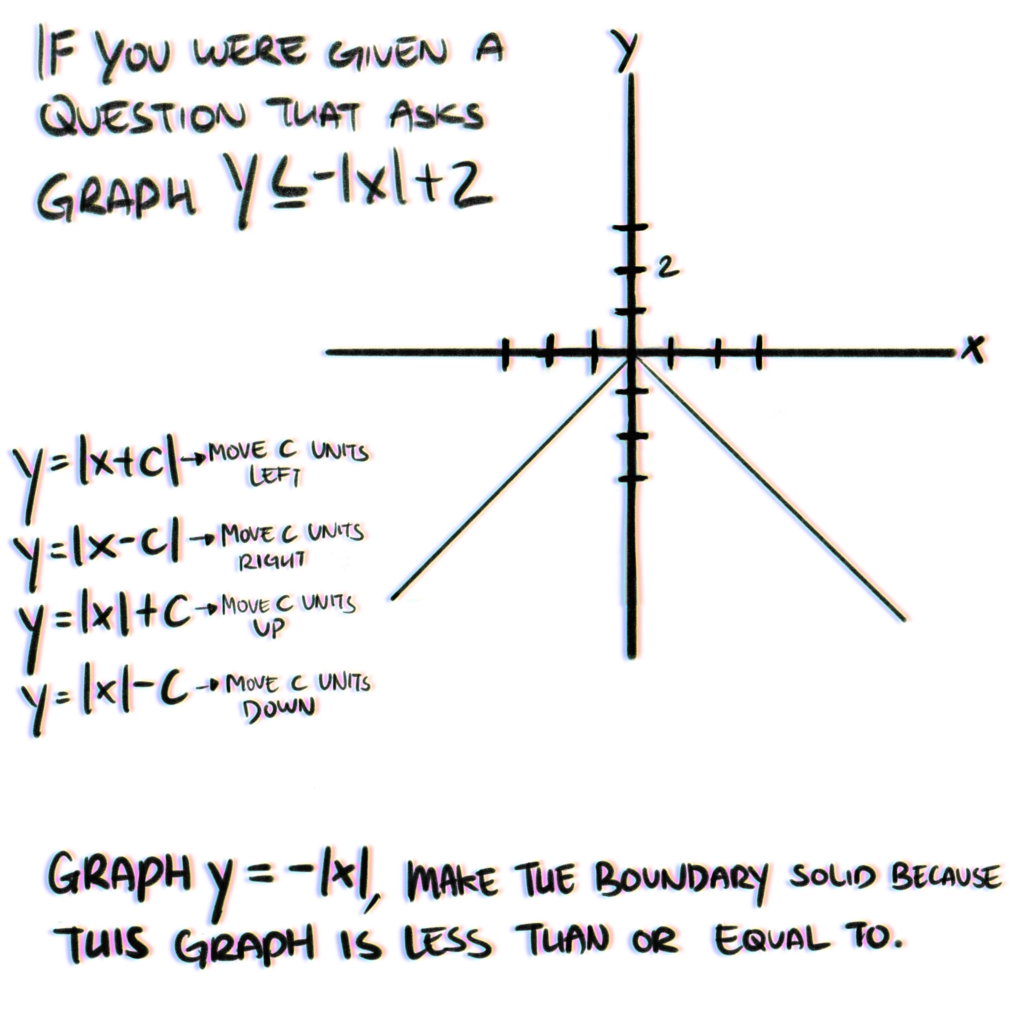
I actually don’t know how this will be applied for real life problems but I learnt it and I will share it with you. What I have learned was about absolute value inequalities with two variables, and sometimes there are questions that asks us to graph the equation after we solve the problem. Take a look at the example below, we have been given a question that asked us to graph y ≤ -|x| + 2. Before we head straight into solving we have to remember some rules or steps before solving the equation, in the image below there are many y = |x + c| or some other form of it, this information helps us determine where the v sign will be located on the graph.

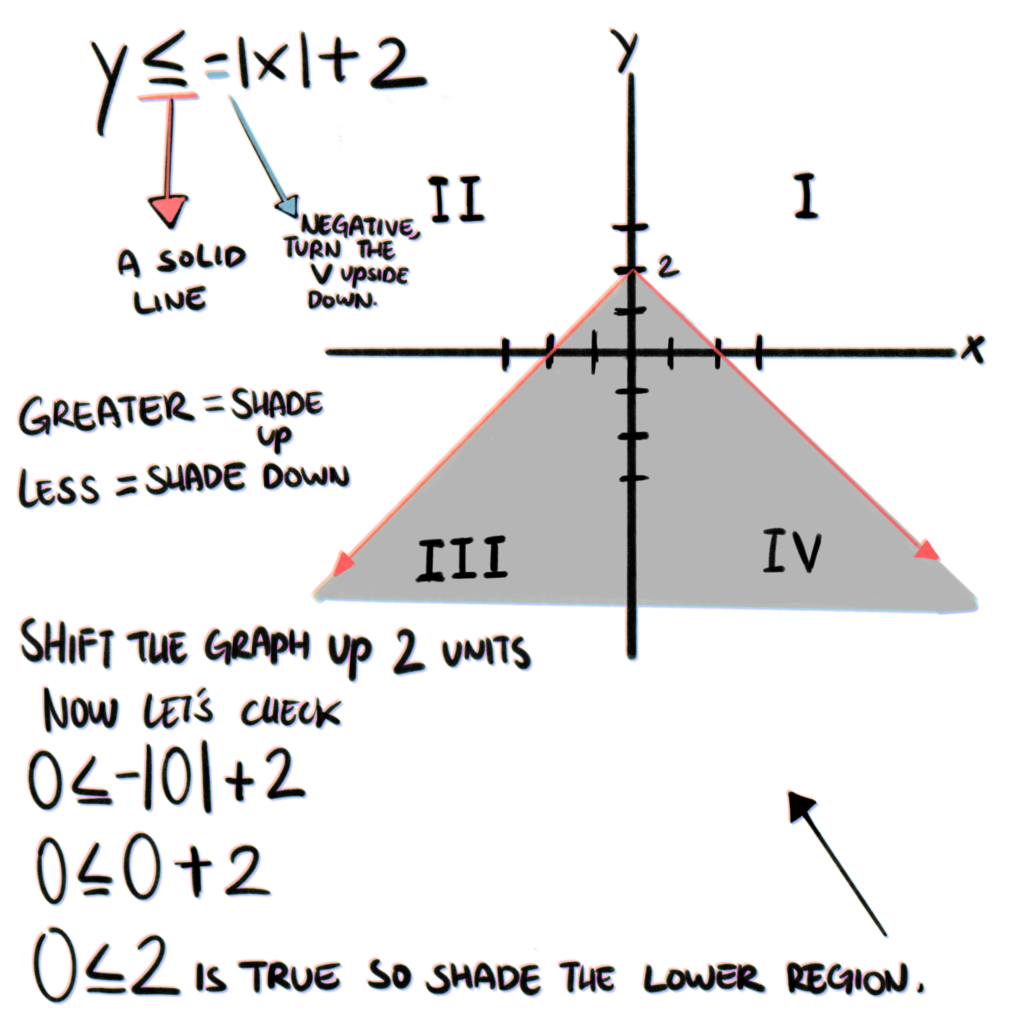
No that we understand the signs let us now solve the equation, we have a sign that says y is lesser than or equal to negative absolute value of x plus 2. The sign lesser than or equal to indicates the the V is a solid like and that we have to shade the lower part of the graph but we have to check if the graph is true before we do that , the negative sign tells us that the v will be flipped facing down too. The upper image shows the V sign originally starts at zero, but now we move it up to two units, finally we check if the equation is true.